Generalized additive models for longitudinal biomedical data

class: title-slide, right, top
background-image: url(img/r_medicine.jpg)
background-position: 10% 75%, 75% 75%
background-size: 30%, cover

.right-column[
# Generalized additive models for longitudinal biomedical data
### _Beyond linear models_

**Ariel Mundo** 
 
Department of Biomedical Engineering University of Arkansas 
08-26-2021
]

---
name: about-me
layout: false
class: about-me-slide, inverse, middle, center

# About me

.pull-left[
<img style="border-radius: 50% 20% / 10% 40%;" src="img/profile pic.jpg" width="200px"/>
### Ariel Mundo
[<svg viewBox="0 0 512 512" style="height:1em;position:relative;display:inline-block;top:.1em;" xmlns="http://www.w3.org/2000/svg"> <path d="M459.37 151.716c.325 4.548.325 9.097.325 13.645 0 138.72-105.583 298.558-298.558 298.558-59.452 0-114.68-17.219-161.137-47.106 8.447.974 16.568 1.299 25.34 1.299 49.055 0 94.213-16.568 130.274-44.832-46.132-.975-84.792-31.188-98.112-72.772 6.498.974 12.995 1.624 19.818 1.624 9.421 0 18.843-1.3 27.614-3.573-48.081-9.747-84.143-51.98-84.143-102.985v-1.299c13.969 7.797 30.214 12.67 47.431 13.319-28.264-18.843-46.781-51.005-46.781-87.391 0-19.492 5.197-37.36 14.294-52.954 51.655 63.675 129.3 105.258 216.365 109.807-1.624-7.797-2.599-15.918-2.599-24.04 0-57.828 46.782-104.934 104.934-104.934 30.213 0 57.502 12.67 76.67 33.137 23.715-4.548 46.456-13.32 66.599-25.34-7.798 24.366-24.366 44.833-46.132 57.827 21.117-2.273 41.584-8.122 60.426-16.243-14.292 20.791-32.161 39.308-52.628 54.253z"></path></svg> @amundortiz](https://twitter.com/amundortiz) 
[<svg viewBox="0 0 496 512" style="position:relative;display:inline-block;top:.1em;height:1em;" xmlns="http://www.w3.org/2000/svg"> <path d="M165.9 397.4c0 2-2.3 3.6-5.2 3.6-3.3.3-5.6-1.3-5.6-3.6 0-2 2.3-3.6 5.2-3.6 3-.3 5.6 1.3 5.6 3.6zm-31.1-4.5c-.7 2 1.3 4.3 4.3 4.9 2.6 1 5.6 0 6.2-2s-1.3-4.3-4.3-5.2c-2.6-.7-5.5.3-6.2 2.3zm44.2-1.7c-2.9.7-4.9 2.6-4.6 4.9.3 2 2.9 3.3 5.9 2.6 2.9-.7 4.9-2.6 4.6-4.6-.3-1.9-3-3.2-5.9-2.9zM244.8 8C106.1 8 0 113.3 0 252c0 110.9 69.8 205.8 169.5 239.2 12.8 2.3 17.3-5.6 17.3-12.1 0-6.2-.3-40.4-.3-61.4 0 0-70 15-84.7-29.8 0 0-11.4-29.1-27.8-36.6 0 0-22.9-15.7 1.6-15.4 0 0 24.9 2 38.6 25.8 21.9 38.6 58.6 27.5 72.9 20.9 2.3-16 8.8-27.1 16-33.7-55.9-6.2-112.3-14.3-112.3-110.5 0-27.5 7.6-41.3 23.6-58.9-2.6-6.5-11.1-33.3 2.6-67.9 20.9-6.5 69 27 69 27 20-5.6 41.5-8.5 62.8-8.5s42.8 2.9 62.8 8.5c0 0 48.1-33.6 69-27 13.7 34.7 5.2 61.4 2.6 67.9 16 17.7 25.8 31.5 25.8 58.9 0 96.5-58.9 104.2-114.8 110.5 9.2 7.9 17 22.9 17 46.4 0 33.7-.3 75.4-.3 83.6 0 6.5 4.6 14.4 17.3 12.1C428.2 457.8 496 362.9 496 252 496 113.3 383.5 8 244.8 8zM97.2 352.9c-1.3 1-1 3.3.7 5.2 1.6 1.6 3.9 2.3 5.2 1 1.3-1 1-3.3-.7-5.2-1.6-1.6-3.9-2.3-5.2-1zm-10.8-8.1c-.7 1.3.3 2.9 2.3 3.9 1.6 1 3.6.7 4.3-.7.7-1.3-.3-2.9-2.3-3.9-2-.6-3.6-.3-4.3.7zm32.4 35.6c-1.6 1.3-1 4.3 1.3 6.2 2.3 2.3 5.2 2.6 6.5 1 1.3-1.3.7-4.3-1.3-6.2-2.2-2.3-5.2-2.6-6.5-1zm-11.4-14.7c-1.6 1-1.6 3.6 0 5.9 1.6 2.3 4.3 3.3 5.6 2.3 1.6-1.3 1.6-3.9 0-6.2-1.4-2.3-4-3.3-5.6-2z"></path></svg> @aimundo](https://github.com/aimundo)
]

.pull-right[
![:scale 30%](img/uark_logo.png) 
Department of Biomedical Engineering 
University of Arkansas Fayetteville, AR, USA
]
---
class: center
This talk is based on work from our lab (under review) the preprint is available at:

![:scale 15%](img/bioRxiv.png)

![:scale 40%](img/preprint.png)

This paper covers:

**Limitations of linear models** 
**Theory of GAMs** 
**Workflow for GAM selection in R using biomedical data** 
https://doi.org/10.1101/2021.06.10.447970

--
 
The slides of this talk are available at 
[tinyurl.com/m75rupjd](https://tinyurl.com/m75rupjd)

---

# Motivation

> Longitudinal studies (LS): Repeated measures on the subjects in multiple groups

> LS are a powerful tools because they allow to see the evolution of an effect over time

> Some examples of different areas of biomedical research that use longitudinal studies:

- Pediatrics

- Cancer

- Nutrition

---

### How do we analyze longitudinal data?

#### What we tend to do in Biomedical Research:

.my-coral[Repeated measures &#8594; repeated measures ANOVA (rm-ANOVA) &#8594; _post-hoc_ comparisons ]

#### Or we can also do:

.green[Repeated measures &#8594; linear mixed model (LMEM) &#8594; _post-hoc_ comparisons]

---
# Simulation to the rescue!

- Some simulated data that follows trends of tumor volume reported in Zheng et. al. (2019). 
--

- Simulation is useful here because we can only get a mean value from the paper. 
--
.pull-left[
<img src="RMedicine2021_slides_files/figure-html/data-plot-1.png" width="504" />
]

--
.pull-right[
<img src="RMedicine2021_slides_files/figure-html/simulated-data-1.png" width="504" />
]

---

### How does an rm-ANOVA model look on this data?

- Linear model with interaction of time and group:

.panelset[
.panel[.panel-name[model]

```r
lm1<-lm(Vol_sim ~ Day + Group + Day * Group, data = dat_sim)
```
Where: 
`Vol_sim`= simulated volume size 
`Day`= Day number (1-15) 
`Group`= Factor (T1 or T2) 
`dat_sim`= simulated dataset

]

.panel[.panel-name[p-values]

```r
anova(lm1)
```

```
## Analysis of Variance Table
## 
## Response: Vol_sim
## Df Sum Sq Mean Sq F value Pr(>F) 
## Day 1 1572512 1572512 554.64 < 2.2e-16 ***
## Group 1 1411668 1411668 497.91 < 2.2e-16 ***
## Day:Group 1 879240 879240 310.12 < 2.2e-16 ***
## Residuals 316 895923 2835 
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

]

.panel[.panel-name[post-hoc]

```r
emmeans(lm1, ~Day * Group, adjust = "bonf")
```

```
##  Day Group emmean   SE  df lower.CL upper.CL
##  7.5 T1       257 4.21 316      248      267
##  7.5 T2       124 4.21 316      115      134
## 
## Confidence level used: 0.95 
## Conf-level adjustment: bonferroni method for 2 estimates
```
]

.panel[.panel-name[Plot]

.pull-left[
<img src="RMedicine2021_slides_files/figure-html/rm-ANOVA plot-1.png" width="504" />
]

.pull-right[
 
![:scale 50%](img/uncle_roger.gif)
]

]
]

---
### But what is exactly an rm-ANOVA?

`\begin{equation}
y_{ijt} = \beta_0+\beta_1 \times time_{t} +\beta_2 \times treatment_{j} +\beta_3 \times time_{t}\times treatment_{j}+\varepsilon_{ijt}\\ 
\end{equation}`

--
`\(y_{ijt}\)`: is the response for subject `\(i\)` in treatment group `\(j\)` at time `\(t\)`

--
`\(\beta_0\)`: the mean group value

--
`\(time_t\)`, `\(treatment_j\)`, `\(time_t \times treatment_j\)`: fixed effects

--
`\(\beta_1, \beta_2\)` and `\(\beta_3\)`: linear slopes of the fixed effects. 
 
--
`\(\varepsilon_{ijt}\)`: random variation not explained by the fixed effects, assumed to be `\(\sim N(0,\sigma^2)\)`

---

### In other words...

An rm-ANOVA is a model that fits a .my-gold[**line**] to the trend of the data!

.pull-left[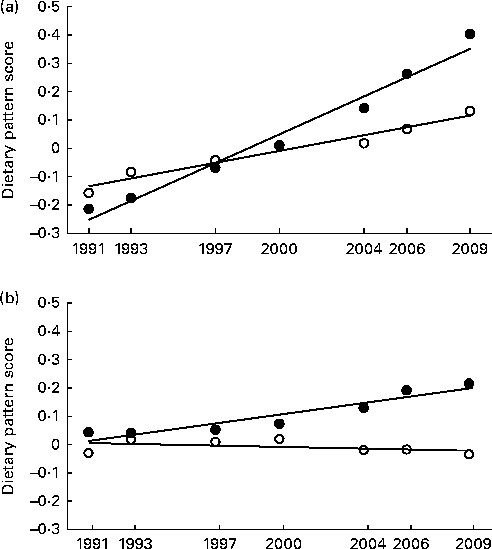
![:scale 75%](img/batis.gif)
]
.footnote[
_Batis et. al. 2013_
]

--
.pull-right[

- It works reasonably well in certain cases

.remark-slide-emphasis[
 .green[
 But in biomedical research things don't look linear!
 ]
 ]
]
---

# Some examples
.pull-left[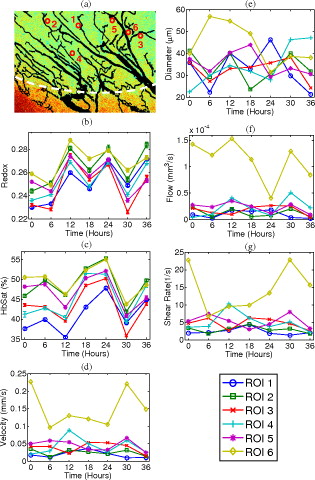
![:scale 50%](img/Skala.jpg)
]
.footnote[
_Skala et. al. 2010_
]

.pull-right[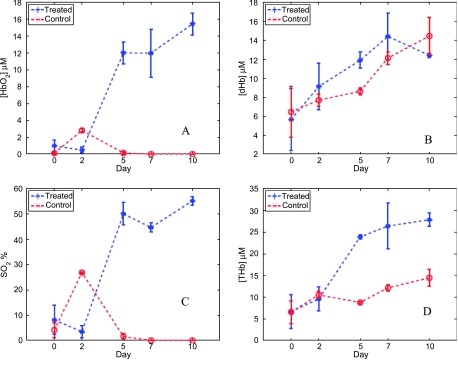
![:scale 80%](img/Vishwanath.jpg)
.footnote[
_Vishwanath et. al. 2009_
]
]

---
# An alternative: Generalized additive models (GAMs)

`\begin{equation}
  y_{ijt}=\beta_0+f(x_t\mid \beta_j)+\varepsilon_{ijt}
\end{equation}`

`\(y_{ijt}\)`: response at time `\(t\)` of subject `\(i\)` in group `\(j\)`

`\(\beta_0\)`: expected value at time 0

The change of `\(y_{ijt}\)` over time is represented by the _smooth function_ `\(f(x_t\mid \beta_j)\)` with inputs as the covariates `\(x_t\)` and parameters `\(\beta_j\)`

`\(\varepsilon_{ijt}\)` represents the residual error

---
# An alternative: GAMs

---

# How does a GAM model look for the simulated data?
.panelset[
.panel[.panel-name[model]

```r
gam1 <- gam(Vol_sim ~ Group+s(Day, by = Group, k = 10),
 method='REML',
 data = dat_sim)
```
]

.panel[.panel-name[Plot]

]

.panel[.panel-name[Pairwise comp.]

.pull-right[
- Comparisons are not guided by a _p-value_

- But the comparison actually makes sense!
]

]

---

# Other advantages of GAMs

- Can use different covariance structures &#9989;

- Work with missing observations &#9989;

- Different types of splines can be used:

- Cubic
 - thin plate
 - Gaussian process

---
# Conclusions

- Doing a visual exploration of the data is always a good idea!

--
- GAMs allow to fit non-linear responses over time

--
- The same idea behind a rm-ANOVA or LMEM holds, but you use a spline instead of a line to do the fitting

--
- .red[_p-values_] can be misleading!

---

class: center

# Acknowledgements

.pull-left[
Dr. John R. Tipton 
Department of Mathematical Sciences, University of Arkansas

Dr. Timothy J. Muldoon 
Department of Biomedical Engineering, University of Arkansas

Silvia Canelon (slides theme)

Alison Presmanes Hill (font, Atkinson Hyperelegible)
https://brailleinstitute.org/freefont
]

.pull-right[
![:scale 20%](img/nsf.png) 
![:scale 45%](img/ABI.png)
]

---

## References

- Batis, C., Sotres-Alvarez, D., Gordon-Larsen, P., Mendez, M., Adair, L., & Popkin, B. (2014). Longitudinal analysis of dietary patterns in Chinese adults from 1991 to 2009. _British Journal of Nutrition_, 111(8), 1441-1451. doi:10.1017/S0007114513003917

- Skala, M. C., Fontanella, A. N., Lan, L., Izatt, J. A., & Dewhirst, M. W. (2010). Longitudinal optical imaging of tumor metabolism and hemodynamics. _Journal of biomedical optics, 15(1)_, 011112.doi: 10.1117/1.3285584

- Vishwanath, K., Yuan, H., Barry, W. T., Dewhirst, M. W., & Ramanujam, N. (2009). Using optical spectroscopy to longitudinally monitor physiological changes within solid tumors. _Neoplasia_ (New York, N.Y.), 11(9), 889–900. doi: 10.1593/neo.09580

- Zheng, X., Cui, L., Chen, M., Soto, L. A., Graves, E. E., & Rao, J. (2019). A near-infrared phosphorescent nanoprobe enables quantitative, longitudinal imaging of tumor hypoxia dynamics during radiotherapy. Cancer research, 79(18), 4787-4797. doi: 10.1158/0008-5472.CAN-19-0530